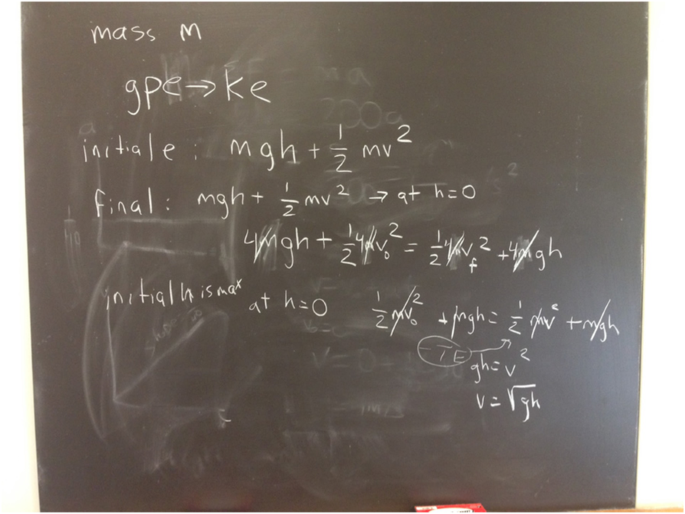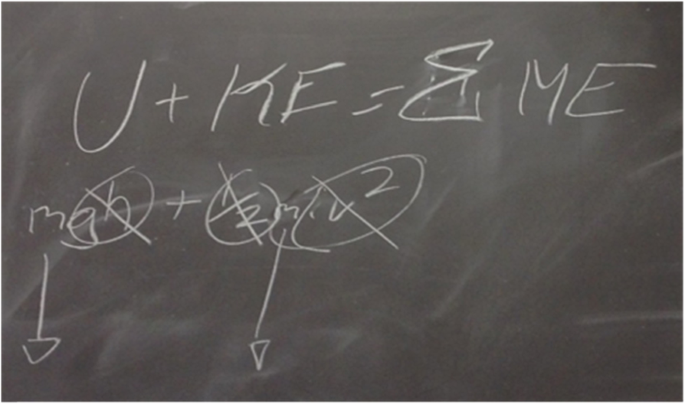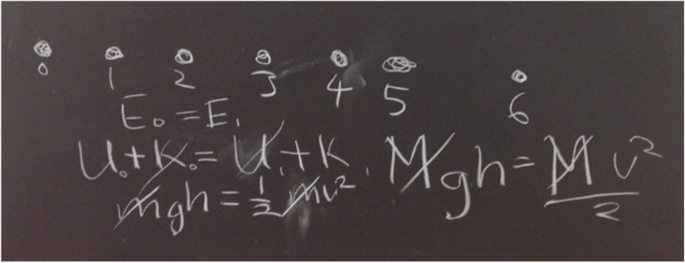- Research
- Open access
- Published:
Students’ problem-solving strategies in qualitative physics questions in a simulation-based formative assessment
Disciplinary and Interdisciplinary Science Education Research volume 2, Article number: 1 (2020)
Abstract
Previous studies on quantitative physics problem solving have been concerned with students’ using equations simply as a numerical computational tool. The current study started from a research question: “How do students solve conceptual physics questions in simulation-based formative assessments?” In the study, three first-year college students’ interview data were analyzed to characterize their problem-solving strategies in qualitative physics questions. Prior to the interview, the participating students completed four formative assessment tasks in physics integrating computer simulations and questions. The formative assessment questions were either constructed-response or two-tiered questions related to the simulations. When interviewing students, they were given two or three questions from each task and asked to think aloud about the questions. The findings showed that students still used equations to answer the qualitative questions, but the ways of using equations differed between students. The study found that when students were able to connect variables to a physical process and to interpret relationships among variables in an equation, equations were used as explanatory or conceptual understanding tools, not just as computational tools.
Introduction
Since the new U.S. science standards, Next Generation Science Standards (NGSS), were released (NGSS Lead States, 2013), science assessments have been moving towards revealing students’ reasoning and their ability to apply core scientific ideas in solving problems (National Research Council, 2014; Pellegrino, 2013). Underwood, Posey, Herrington, Carmel, and Cooper (2018) suggested types of questions aligned with three-dimensional learning in A Framework for K-12 Science Education (National Research Council, 2012). These questions include constructed-response (CR) questions and two-tiered questions. Underwood et al. (2018) also argued that questions should address core and cross-cutting ideas and ask students to consider how scientific phenomena occur so that they can construct explanations and engage in argumentation. The underlying assumption of this approach could be that qualitative explanation questions (i.e., questions that ask students to explain qualitatively) reveal students’ reasoning and understanding of core scientific concepts better than do traditional multiple-choice and simple-calculation questions. Numerous studies in physics education have examined students’ problem-solving strategies, including studies that have identified differences in the problem-solving strategies employed by experts and novices. Experts tend to start by using general scientific principles to analyze problems conceptually, while novices tend to start by selecting equations and plugging in numbers (Larkin, McDermott, Simon, & Simon, 1980; Maloney, 1994; Simon & Simon, 1978). Thus, giving students opportunities to reason qualitatively about problems could help them to think like experts (van Heuvelen, 1991).
Another way to enhance students’ conceptual understanding of scientific ideas could be using computer simulations, because computer simulations help students visualize scientific phenomena that cannot be easily and accurately observed in real life. Many empirical studies support integrating computer simulations into assessments in order to promote students’ engagement in exploring scientific phenomena (de Jong & van Joolingen, 1998) and their conceptual understanding (Rutten, van Joolingen, & van der Veen, 2012; Trundle & Bell, 2010). For example, Quellmalz, Timms, Silberglitt, and Buckley (2012) developed a simulation-based science assessment, and found that the assessment was effective to reveal students’ knowledge and to find evidence of students’ reasoning. In the current study, computer simulations and conceptual qualitative questions were incorporated as integral parts of formative assessment to reveal students’ problem-solving strategies in answering qualitative physics questions. Therefore, the current study investigated students’ problem-solving strategies in physics, which offered them opportunities to elicit their reasoning by qualitatively explaining what would happen and why it would happen about a given physical situation.
Students’ strategies to solving physics problems
Early research on physics problem solving identified differences between experts and novices in their problem-solving strategies. For example, experts’ knowledge is organized into structures; thus, they demonstrate the effective use of sophisticated strategies to solve problems (Gick, 1986). Conversely, novices tend to describe physics problems at best in terms of equations, and spontaneously use superficial analogies (Gick, 1986). Experts also effectively use the problem decomposition strategy: breaking down a problem into subproblems, then solving each subproblem and combining them to form the final solution (Dhillon, 1998). They also apply relevant principle and laws to solve problems (Chi, Feltovich, & Glaser, 1981; Dhillon, 1998). By contrast, novices start with selecting equations and cue into surface features (Chi et al., 1981). A common finding from studies on differences between experts and novices in problem solving (e.g., Chi et al., 1981; Dhillon, 1998; Gick, 1986; Larkin et al., 1980) is that experts demonstrate their expertise in conceptual analysis of the problems using scientific principles and laws, then translate the problem into relevant mathematical equations, while novices jump to mathematical manipulations without the prior process of conceptual analysis (Larkin et al., 1980).
Huffman (1997) incorporated the results of studies on the differences in problem solving between experts and novices to formulate explicit problem-solving procedures for students. The procedures include five steps: (a) performing a qualitative analysis of the problem situation; (b) translating the conceptual analysis into a simplified physics description; (c) translating the physics description into specific mathematical equations to plan the solution; (d) combining the equations according to the plan; and (e) evaluating the solution to ensure it is reasonable and complete (Huffman, 1997). In essence, the procedure is designed to ensure students will conceptually reason about the problem first, using relevant scientific principles and laws, before jumping to selecting mathematical equations.
It is possible that students’ problem-solving strategies are influenced by problem representations (verbal, mathematical, graphical, etc.). Kohl and Finkelstein (2006) investigated how problem representations and student performance were related, and found that student strategies to solve physics problems often varied with different representations. They also found that not only problem representations but a number of other things, including prior knowledge and experience in solving problems from their previous classes, also influenced students’ performance, especially in the case of low-performing students. When asking students not to calculate a science question but to explain it conceptually, a study found that they still used equations or numerical values to solve the problems, indicating that they translated a conceptual qualitative question into a quantitative one (De Cock, 2012). Although students may succeed in calculating values in physics problems, it doesn’t always mean that they have good conceptual understanding of the questions (McDermott, 1991).
While earlier studies have been concerned with students’ using equations without conceptual understanding when solving problems, mathematical modeling plays a critical role in the epistemology in physics (Redish, 2017). Redish emphasized the importance of connecting physical meaning to mathematical representation when solving problems, because in physics, mathematical equations are linked to physical systems, and an equation contains packed conceptual knowledge. Thus, in physics, equations are not only computational tools but also symbolic representations of logical reasoning (Redish, 2005, 2017). As such, students are expected to incorporate mathematical equations into their intuition of the physical world to conceptualize the physical system (Redish & Smith, 2008). In a study of students’ quantitative problem solving, Kuo, Hull, Gupta, and Elby (2012) pointed out the importance of connecting mathematical symbols to conceptual reasoning. Their study was conducted based on an assumption that equations should be blended with conceptual meaning in physics, which turned the attention of researchers on problem solving from how students select equations to how they use the equations. Kuo et al. (2012) concluded that blending of mathematical operations with conceptual reasoning constitutes good problem solving; thus, this blended process should be a part of problem-solving expertise in physics.
Using computer simulations as an assessment tool
Given that visualization plays a central role in the conceptualization process of physics (Kozhevnikov, Motes, & Hegarty, 2007), previous studies have used computer simulations to visualize scientific phenomena, especially those that cannot be accurately observed in real life, and reported their positive effect on students’ learning outcomes (Ardac & Akaygun, 2004; Dori & Hameiri, 2003). Using computer simulation to facilitate student learning in science was found to be especially effective on student performance, motivation (Rutten et al., 2012), and conceptual change (Smetana & Bell, 2012).
Computer simulation can be used not only as an instructional tool but also as an assessment tool. For example, Park, Liu, and Waight (2017) developed computer simulations for U.S. high school chemistry classes to help students conceptualize scientific phenomena, and then integrated the simulations into formative assessments with questions related to the simulations. Quellmalz et al. (2012) and Srisawasdi and Panjaburee (2015) also embedded computer simulations into formative assessments for use in science classrooms, and demonstrated positive effects on students’ performance compared to students who experienced only traditional assessments (e.g., paper-and-pencil tests). While many empirical studies have been done to investigate problem-solving strategies of students, there is a lack in studies on students’ strategies to solve physics problems when computer simulations were used as a visual representation and conceptual explanation questions were asked to reveal the students’ reasoning. This study addresses the gap in the body of literature by investigating students’ strategies in solving conceptual explanation questions in a simulation-based formative assessment.
Methods
Research procedure and participants
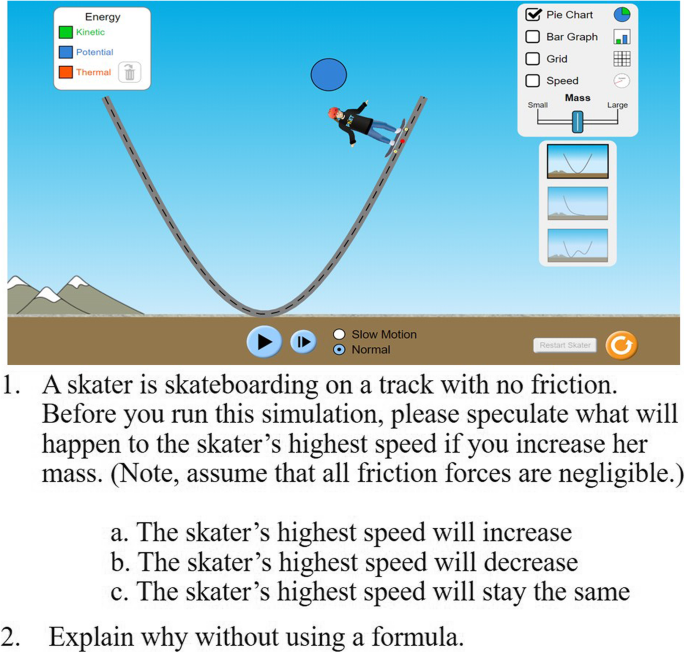
In the study, computer simulations and formative assessment questions were integrated into a web-based formative assessment system for online administration, which allowed students to use it at their convenience (Park, 2019). The formative assessment questions were either CR or two-tiered questions related to the simulations. A two-tiered question consists of a simple multiple-choice (MC) question and a justification question for which students write a justification for their answer to the MC question. This format of question was suggested to diagnose possible misconceptions held by students (Treagust, 1985) and to provide information about students’ reasoning behind their selected responses (Gurel, Eryılmaz, & McDermott, 2015). Computer simulations were selected from the Physics Education Technology (PhET) project (https://phet.colorado.edu/) and embedded into the formative assessment system. The assessments targeted students’ conceptual understanding in physics, thus they were not asked to calculate any values or to demonstrate their mathematical competence (Park, 2019). Specifically, the questions presented a scientific situation and asked students to predict what would happen; then the assessment system asked students to run a simulation, posing questions asking for explanation of the phenomena and comparison between their prior ideas and the observed phenomena. Figure 1 presents example questions and simulation for the energy conservation task. After answering the questions, students ran the simulation and responded to questions asking how the skater’s highest speed changed and why they think it happened using evidence found in the simulation.
Initially, first-year college students were recruited from a calculus-based, introductory level physics course at a large, public university in the United States; no particular demographic was targeted during recruitment. The physics course was offered to students majoring in subjects related to science or engineering and covered mechanics, including kinematics and conservation of energy, so simulations were selected to align with the course content. After selecting simulations from the PhET project, related formative assessment questions were created. As previously mentioned, the questions first asked students to predict what would happen in a given situation. In this case, verbal (expressed in writing) and pictorial representations (including images, diagrams, or graphs) describing the situation were shown on the screen (Fig. 1). Next, after the students answered the questions, the simulations were enabled for the students to run, and they were asked to explain the results. In total, four formative assessment tasks were developed and implemented online, and each task contained from 14 to 17 questions. Topics for the four tasks were (1) motion in two dimensions, (2) the laws of motion, (3) motion in one dimension and friction, and (4) conservation of energy. Descriptions of the four tasks are presented below.
Task 1: Students explore what factors will affect an object’s projectile motion when firing a cannon.
Task 2: Students create an applied force such as pulling against or pushing an object and observe how it makes the object move.
Task 3: Students explore the forces at work when a person tries to push a filing cabinet on a frictionless or frictional surface.
Task 4: Students explore a skater’s motion on different shapes of tracks and explore the relationship between the kinetic energy and thermal energy of the skater.
After the participating students completed the online implementations of the four tasks, an interview invitation email was sent to the students who had completed all four tasks, did not skip any questions, and did not answer a question with an off-task response, but included responses that needed further clarification. Initially, we invited six students to clarify and elaborate on their responses so we could better understand what they were thinking. When scoring students’ written responses, some responses needed further clarification. For example, students mentioned that in projectile motion, “mass is not relative to time”; “the greater angle will create a larger x component of velocity in a projectile motion”; or “an object’s speed is broken up evenly resulting in more air time”. In case of the energy conservation task, the responses needing more clarification were “the speed did not change because speed does not depend on mass” or “because a skater’s total energy increases with increase in mass, her speed does not change”. Those responses were not clear to the author. Thus, the author decided to invite them to clarify their responses. During the interviews, the students’ verbal responses inspired the author to explore differences in their problem-solving strategies to answer conceptual physics questions. Three students especially, Alex, Christopher, and Blake (all pseudonyms), demonstrated noticeable differences in their problem-solving strategies; therefore, they are the focus of the analysis in the current study.
Interview context and protocols
Semi-structured interviews were conducted to investigate students’ reasoning when responding to conceptual physics questions. To this end, the students were given two or three questions from each task and asked to think aloud about the questions. After they verbally answered each question, they were given their original written responses to see if their answers had changed, and if so, to explain why. When students used mathematical equations or graphs in their explanations, they were asked to explain why they used those particular strategies and how the strategies helped them to answer the questions. Some example interview questions were; “Please read the question. Will you tell me your answer for the question?”, “How did you answer this question?”, “Could you clarify what this means?”, and “What did you mean by (specific terms that students used)?” Students were interviewed individually by two interviewers. The interviews, which took place in an interview room located at their university, each lasted an hour.
Analysis
While the interviews were going on, the author wrote memos about the students’ strategies to answer the given questions and their misconceptions about science. Interviews were audio recorded and transcribed verbatim. The transcripts were initially analyzed to prepare and organize data into emergent themes. In this process, the memos were also used. As a result, three initial themes were developed: 1) students’ strategies to answer problems, 2) effects of the assessment on students’ learning, and 3) students’ misconceptions about science. In the study, the first theme—strategies to answer problems—was made a focus in the next level of analysis, as the students demonstrated noticeable differences in using equations to answer conceptual physics problems. After choosing the theme as a main focus, the author analyzed it by open coding the relevant parts of the transcripts of the individual student interviews (interviews about Tasks 1–3) to formulate possible characterizations of students’ problem-solving strategies, especially when they were using equations. The author constantly compared the characterizations to integrate and refine them (Strauss & Corbin, 1998). After that, the rest of each individual student interview transcript (interviews about Task 4) was analyzed, using the same categories to confirm the findings. Students’ drawings (i.e., graphs) used to explain their reasoning were also considered as a data source (Creswell, 2016). Once characterizations in students’ use of equations in qualitative physics question were identified and compared across cases, the analysis results were given to a physics education researcher to seek an external check (Creswell & Miller, 2000).
Findings
Previous studies on expert and novice problem-solving strategies were reflected in the design of the formative assessment questions. Specifically, it was hypothesized that conceptual explanation questions would help students think about the questions more conceptually, so that they would start to solve them using scientific concepts and laws. Therefore, short written questions in the tasks asked the students to explain or to justify their answers without using a formula. Nonetheless, when we were interviewing students, we found that they preferred to use equations and mathematical concepts when explaining physical situations. Although the three participating students commonly used equations or mathematical concepts in their explanations, how they used the equations or mathematical concepts differed. Detailed findings are presented below in three subsections representing patterns in problem-solving strategies. Formative assessment Tasks 1, 2, and 3 were designed to address the topic of Motion and Force, while Task 4 covered the topic of Energy Conservation. We analyzed interview data by these two topics. Note that two terms—formula and equation—were not differentiated in the analysis of data; instead, they were considered synonyms.
Alex’s case – using equations as a conceptual understanding tool
Motion and force
When interviewing Alex, we asked him what would happen if a person pushed a box, then let it go (Task 2). He said, “If it is frictionless, the box will move forever with a constant velocity, and if friction exists, the speed will decrease and eventually the box will stop.” This answer was very similar to his original written response. Next, we asked what would happen to the box’s motion after another box was placed on top of it. Alex said, “I don’t know how to explain this without a formula.” Because the original questions had asked students not to use formulas, he assumed that he was not allowed to use one in this explanation, and obviously he was struggling to explain without it. We told him to use formulas whenever he wanted, and he quickly jumped into using one.
Alex: Resultant force equals mass times acceleration, so if you have a bigger mass. Uh, if the resultant force was 50N, that’s the force you applied, and then you had 10N in friction, for example, then the resultant force is 40. You had, if you had 20kg, the acceleration would be 2. If you had 50kg, the acceleration would be 4 over 5, which is 0.8, which is less than 2. So, the more mass you have the smaller the acceleration is going to be, as a result of the resultant force equals ma equation.
In this statement, Alex explained what would happen in the given situation with algebraic solutions, using F = ma equation, and concluded that mass would affect the object’s acceleration, as he demonstrated. He further described how the eq. (F = ma) helped him to explain the given physical situation.
Alex: If you use the formula, then it makes it much easier, because in real life, you never see something moving without friction, so it just clouds your judgment a bit.
In this statement, Alex described the role of equation for him as a conceptual understanding tool, especially in an ideal situation that is not observable in real life. This was something the author had not initially expected from the students during their interviews. When we asked Alex the next question in Task 3, his answer further supported the finding that equations helped him understand physical situations. Specifically, we asked, in a situation when a person was pushing a cabinet on either a frictionless or a frictional surface, what would happen to the cabinet’s motion and why.
Alex: The normal force is, the gravitational force cancels out the y, so the only thing acting on the—in the x-direction, which is the direction being pushed is the applied force, so as small of a force you apply to it, it’s still going to move it because there’s nothing opposing it…if there was friction, I agree that it won’t move. Because the friction, the friction is the coefficient of friction times the normal force, so, since it’s a really big object, it’s going to have a significant amount of friction acting on it.
In his verbal explanation, Alex used a mathematical concept and an equation to explain the given phenomenon, using the vector concept for two components of force and a mathematical equation for frictional force. Obviously, he found equations useful to make sense of physical situations and to explain his understanding to others. Notably, he started his answer by referring to the formula for kinetic friction force and used the formula as a tool to explain why the cabinet wouldn’t move on a frictional surface. His explanation again demonstrated that equations and mathematical concepts were useful to understanding and interpreting scientific phenomena, and not only as a simple computational tool, at least for Alex.
Conservation of energy
Task 4 was designed to investigate students’ conceptions of mechanical energy and its conservation. We asked Alex, when a skater is skateboarding on a track with no friction, what would happen to the skater’s highest speed as the skater’s mass increases? He again asked us if he could use equations. We confirmed that he was allowed to use equations anytime he wanted. Then he immediately started writing equations on the board (see Fig. 2). While he was writing, he explained each variable involved in the equations:
Alex: So, her initial, so, um, at the start, her initial energy is mgh + ½ mv02 and then her final [writing on board] mgh + ½ mvf2, but the smaller thing to do is that they [mass] all cancel out, so the mass is really, it doesn’t play a role in the height or the velocity. And then, if you wanted to see how the conversion of energy works, if you were initially starting at the maximum height, whatever that is, you could do ½ mv2. At the start, her velocity is 0, at the top, so this cancels out, if we’re analyzing it at the bottom, which is her max speed, then this [h] is 0, and then you just do gh = v2. To find her velocity. Just looking at this, there’s no mass in this, so it doesn’t matter [the skater’s speed]. When you actually work it out, all the masses cancel out, so it doesn’t matter what the mass is, in reality, when you actually calculate it.
This response was different than his original written response to the same question: “If the skater has a larger mass, she will in turn have a larger gravitational potential energy since GPE [gravitational potential energy] has a direct relationship to mass. As a result and according to the principles of conservation of energy, the KE [kinetic energy] will be greater and thus the velocity will be greater.” In this original written response, Alex included a typical misconception that heavier objects fall faster (e.g., Gunstone, Champagne, & Klopfer, 1981; Lazonder & Ehrenhard, 2014); “If the skater has a larger mass…thus the velocity will be greater” (in his written response). This was the only case of a misconception found in Alex’s written responses. Notably, when he was using equations, he deduced that “it doesn’t matter what the mass is, in reality, when you actually calculate it” from his step-by-step problem-solving procedure using algebraic solutions. Although he solved the problem using equations through algebraic computation, he explained how the object’s velocity and height would change as the object moved: “At the start, her velocity is 0, at the top, so this cancels out, if we’re analyzing it at the bottom, which is her max speed, then this [h] is 0, and then you just do gh = v2.” Then he connected conceptual meaning to the equation: “Just looking at this, there’s no mass in this, so it doesn’t matter [the skater’s speed].” This confirmed that for Alex, equations were the first tool to make sense of physical situation. In other words, when he applied an equation to a physical situation, he considered variables related to specific situations, then connected conceptual meaning to the variables, which indicated that for him, equations played a role in analyzing and understanding physical situation.
Christopher’s case – using equations as an explanatory tool
Motion and force
We asked Christopher a question—which tank shell would go farther when the initial angles for two tank shells were different (Task 1). In his original written response, he mentioned that “tank A (initial angle: 45 degree)’s speed is broken up more evenly and this results in more air time which leads to more distance covered in the x axis as well.” This answer was similar to Christopher’s thinking-aloud response, so we asked him to elaborate on what he meant by “speed is broken up more evenly.” Below is his response.
Christopher: Because the velocity is a vector quantity, the speed is still the same, but the velocity, the x and y axis are going to be more evenly split [for Tank A, with a 45-degree initial angle], whereas for Tank B [10-degree initial angle] it would have been almost all in the x axis and close to none in the y, so it wouldn’t get that much air time because the force of gravity still stays the same.
As seen in his response, Christopher deduced his answer from a mathematical concept (vector in this case) explaining why the 45-degree shell would have a greater horizontal range than the 10-degree shell one. His problem-solving strategy in the next questions (questions from Tasks 2 and 3) further confirmed that he used mathematical concepts and equations to explain physical situations. For example, when asked to compare two situations from Task 2—a person pushes a box and lets it go, and after placing another box on top of that, a person pushes both boxes and lets them go—Christopher immediately used F = ma and explained the situation.
Christopher: The velocity and the speed will be decreased because, when applying force, force is mass times acceleration. So, if it would be the same exact force with a higher mass, then the acceleration would have to go down significantly in order to keep the same number [force]. So, because of this, it wouldn’t speed up as much, so it would have a lower velocity after the force was applied [compared to the previous situation]. While you are pushing, the acceleration is constant. And if they let it go, there is no acceleration. Then speed will stay the same.
In his statement, he referred to F = ma, and explained why the box’s acceleration would be smaller when its mass increased using algebraic solutions, which is similar to Alex’s case. The difference is that Christopher’s explanation contained an interpretation of the relationship among velocity, acceleration, and applied force: “So, because of this, it wouldn’t speed up as much, so it would have a lower velocity after the force was applied.” This implies that Christopher did not just use the equation as a computational tool, but linked meanings to variables (force, velocity, mass, and acceleration) and interpreted a relationship among them. When we asked him a question from Task 3—when a person is pushing a cabinet, how will the cabinet’s velocity change after passing over the frictionless surface and traveling onto the surface with friction?—his answer reconfirmed that he considered the relationship among variables and gave conceptual meaning not only to the variables but also to the relationship, and used a mathematical concept as an important tool to interpret a physical situation.
Christopher: So, the velocity is 100% dependent on the acceleration, which depends on the force, and then in this scenario, it is the force at first, it has a much higher total net force in the x direction, whereas later on it decreases [on a frictional surface], but there’s still a positive net force in the x direction, so it will continue. The reason why it continues to speed up is because the acceleration is still positive. ‘Cause mass can’t really be negative so that [acceleration] is the only variable [to determine the change of velocity]. So, that’s why velocity continues to increase, it’s just not as much as before.
In his statement, Christopher did not interpret an individual variable separately; rather, he first considered the relationship between force, velocity, and acceleration using the concept of vector and scalar quantity (e.g., mass is not a vector quantity), and explained how each variable was influenced by the other variables’ changes. From the statements above, it is clear that Christopher reasoned through a physical process by interpreting relationships among variables and attaching conceptual meaning to the relationship and the variables.
Conservation of energy
When we asked Christopher about change in the skater’s highest speed when the skater’s mass increased, his original written and oral responses contained the common answer that the skater’s highest speed would stay the same because gravity acts on all objects equally: “the downward acceleration will be the same.” We further asked him about how total mechanical energy changes. His response is below.
Christopher: Her [the skater’s] mechanical energy would increase because the velocity would stay the same for kinetic, but the mass would go up, so it would make the answer higher. And it’s probably easier to think of it with GPE, can I use the formula to it?
Then he drew a formula on board (Fig. 3), and explained why the total mechanical energy would change.
Christopher: This is mg. Since these two [gh, ½] stay the same for both cases, they can be canceled out. So then, these are the only variables in ME (mechanical energy), so if this [m] increases, then the whole system[’s energy] will increase, but it won’t change this [v] in the specific scenario. If you were to use the equations, once you were to set them equal to each other and solve for the final answer for each, they would still be the same, even though the mass is higher. But because it’s multiplied, you can cancel it [m] on both sides for that specific scenario, so it mainly just depends on the constant ½ and then the variable of height and the final velocity which would be the same for this case.
In his response, Christopher first explained the physical situation using the concept of energy and considered the situation as a system: “Her [the skater’s] mechanical energy would increase,” and “so if this [m] increases, then the whole system[‘s energy] will increase.” In order to prove why mass doesn’t affect the skater’s speed, he used an equation as an explanatory tool—“And it’s probably easier to think of it with GPE, can I use the formula to it?”—and showed that mass doesn’t affect the skater’s speed: “You can cancel it [m] on both sides for that specific scenario.” A noticeable difference from Alex’s approach is that Christopher used equations to prove his claim and to explain it in an easier way, while Alex used equations to make sense of the situation. In other words, equations were in play mainly as explanatory tools for Christopher, whereas they acted as conceptual understanding tools for Alex. Similarly to his previous responses to questions in Motion and Force, Christopher again demonstrated that he considered how all variables were related each other in the system, and attached meaning to the relationship and variables. Interestingly, he often used the phrase “specific scenario,” so we asked what it meant. Below is his response.
Christopher: The equations don’t really help because even though I see it and it’s in my head, but it’s not really useful if I don’t know the scenario. If it’s some problems, I know, are purposefully shaped to muddle it up, and make it purposefully confusing, but usually, when you run the scenario, in a program or in your head, it kind of takes out that confusing stuff.
The above response illustrated that Christopher conceptually interpreted the physical situation first, then translated equations into the physical situation. This strategy shared a commonality with Alex’s in that both students used equations in their explanations and connected how variables in the equations changed as the specific physical situation changed. At the same time, there was a difference between the two students. Christopher’s strategy started with an analysis of the situation, creating a physical scenario and then translating equations into the physical situation, while Alex mentioned relevant equations first, then connected them to the physical situation.
Blake’s case – using equations as a computational tool
Motion and force
When we asked Blake which one would go farther when shot from a cannon, a tank shell or a baseball (when air resistance was negligible; Task 1), her original written response and her thinking-aloud response were similar: the mass of an object is not relative to its motion. When we asked her to explain why, she said:
Blake: Because I don’t see kg on the units at all [in the simulation]. kg is the unit for mass, kilograms, so, it’s not written as kg/m/s or something. You could easily compare it with units and mass is not part of the unit.
Her response was interesting in that she used the unit of velocity rather than acceleration. Also, she did not show her conceptual understanding of physical variables and their relationship as Christopher had done. We further asked her what factors should be changed to maximize the horizontal range of the projectile object, in order to elicit her reasoning about a projectile motion. Below is her response.
Blake: You need to throw it faster. Um, because, if you look at gun for example. It’s a really high velocity. So, you just see it going like straight because it’s just high velocity. And, um, if, if I’m throwing this phone, maximum distance it could go is like here [tosses phone, not very far]. Angle? I think…like the maximum distance for x axis and y axis is 45 degrees, but I think it should be a little lower. Around 45 but plus or minus 5 degrees, so like 40 degrees.
Interviewer: Why would you say that?
Blake: It doesn’t get that much time for vertical velocity, but the horizontal velocity will be faster.
In her response, Blake used real-life examples—shooting a gun and throwing a phone—as analogies to reason how to increase the horizontal range of a projectile object. However, when she threw the phone, she tossed it, which started it with a different initial angle from that of a bullet shot from a gun: “You just see it going like straight because it’s just high velocity.” Although she considered two directions of velocity when determining the optimal initial angle, she did not provide a scientifically reasonable explanation for why the initial angle should be lower than 45 degrees. It might be that Blake had learned that 45 degrees is the angle used to maximize range, but that she thought velocity would be more critical than the angle to determine the range, especially that the x-component of velocity would more important than the y-component because an object will fly faster horizontally than vertically when the x-component is greater. Thus, she lowered the initial angle a little bit. In the above statements, Blake did not demonstrate that she could consider the relationship between variables and link conceptual meanings to them (e.g., “Because I don’t see kg on the units at all” and “It doesn’t get that much time for vertical velocity, but the horizontal velocity will be faster”).
For the next question, we asked what would happen to the box’s motion after another box was placed on top of it. She said, “It would still be constant and stay at constant velocity in that motion.” We asked the question again, to clarify if she understood it.
Blake: Yeah. The velocity would be the same. After you let it go. So it will be at constant speed. And the force is proportional to the...wait, well acceleration is proportional to force and mass.
In her response, Blake attempted to apply Newton’s second law (F = ma), as the other two students had; however, she didn’t realize that acceleration is inversely proportional to mass, and therefore the velocity would be changed by the different acceleration. As a result, her response involved a misconception that mass doesn’t affect the speed of an object. In other words, she demonstrated her lack of understanding of the relationships between the variables (acceleration, velocity, mass, and force) involved in the situation. Her response to the questions confirmed that she explained scientific phenomena using variables in equations but failed to recognize the relationships among them. Instead she focused on individual variables, e.g., how acceleration will change as force changes, but did not explain how that would change velocity. She also did not explain how two components of velocity affect an object’s motion. Interestingly, she also used the unit of variable to justify her answer without applying conceptual meanings to it. For Blake, equations and units seemed to play important roles in explaining physical situations, but her connection of equations to physical situations was, at best, based on interpretations of individual variables.
Conservation of energy
When we asked Blake about change in the skater’s highest speed when the skater’s mass increased, her original written response was that her highest speed would increase because the mass of the skater would require more energy. When we interviewed her, her answer was different from her original response.
Blake: I think it should stay the same. I was thinking of the formula.
When we asked her to explain in more detail, she wrote an equation on the board (Fig. 4) and explained what it meant.
Blake: The highest point, because there won’t be any kinetic energy. And it’ll be mgh. Also ½ mv2 and it [m] cancels out. It was exactly the same. The speed was the same. But—wasn’t there a bar graph [in the simulation]? Well, the total energy was bigger [in the simulation]. The total energy. But the total energy was same—no bigger.
Similarly to Alex, Blake used an equation to explain that the skater’s speed wouldn’t change because v doesn’t contain m after canceling out. However, she did not describe why kinetic energy is zero at the highest point and why potential energy is zero at the bottom. It might be that she just did not mention this, but it was obvious that she did not understand how the object’s mass affected the system: “But the total energy was same—no bigger.” We further asked her how the total mechanical energy of the skater would change when the skater’s mass increased. This time, she said, “Well, the total energy was bigger. ‘Cause energy depends on mass and either height or speed of a person.” As seen in the response, she thought of variables in equations of gravitational potential energy (mgh) and kinetic energy (\( \frac{1}{2} \) mv2). When asked why she previously had said the total mechanical energy would be the same, she answered, “because energy is always conserved.” This illustrated her misconception that the amount of energy should always be the same regardless of mass; however, when she considered variables in equations of PE and KE, she answered the question accurately. Throughout the interview, we found that Blake’s strategy to solve questions was consistent across different tasks; she used formulas and units as her first approach. However, a difference between Blake and the other two students is that although she used equations and variables, she did not explain how the variables influenced each other; and how they would change as a specific situation changed. In other words, she did not translate equations into physical situations nor link conceptual meanings to the variables and the relationships between them. The findings showed that for Blake, equations were more likely used as a simple computational tool.
Disconnection of students’ problem-solving strategies from physics lecture
The three students all mentioned that they liked simulation-based questions. Alex said that the questions themselves made him think a lot, and running simulations also made him think more deeply: “Beforehand it [the task] just seems really simple, so you don’t put much thought into it. That’s easy. Just write it down, but then, once you run it, it makes you think about it more. So that’s cool too.”
As seen in his responses to the questions in the tasks, Alex used equations as conceptual understanding tools consistently across tasks. When we asked if he had learned this approach from his physics course, he said that his physics class heavily focused on solving problems but mostly by just reading off equations and plugging in numbers.
Alex: Physics is not about reading equations and stuff off a slide. It’s about working things by hand, and my professor, he has all the solutions to the problems in the book. He had them on a clear sheet of paper, and a Sharpie and then, so if he has problem 20, he puts problem 20 on the projector, and then he put that clean sheet there, and then he points to, oh here I did “v = a + blah blah,” so that’s really not effective at all in my opinion.
Christopher mentioned that the formative assessment would be very helpful for a lot of students, because it showed physical scenario. His physics class was more formula-based, with activities such as showing a formula and plugging in numbers to demonstrate how to solve a physics problem, which Christopher felt was disconnected from how he learned science. As he demonstrated, he learned best when he created a physical scenario, then translated it into equations. Alex also mentioned that physics is “about working things by hand,” which implies that he emphasized linking problem-solving procedures to physical situations. In Blake’s case, she mentioned that “It will help students to learn the concept better, but I think students will hate it [the formative assessment] because students will be like, ‘I don’t have time for this. It’s just that I am like too busy for this.’” In sum, the three students had a common opinion that the simulation-based formative assessment had helped them understand the given physical situation better, but the reasons why they liked it differed, as did their problem-solving strategies.
Discussion and conclusion
Previous studies on problem solving were concerned with students’ using equations simply as numerical computational tools by plugging in numbers. While experts tend to start with a conceptual analysis of problems using scientific principles and laws, novices start by selecting and manipulating equations without conceptual analysis (Larkin et al., 1980). The difference in solving problems might be more obvious in quantitative questions, in which a mathematically framed physics question may prompt students to use equations without conceptual understanding (Kohl & Finkelstein, 2006). The current study started from the research question “How do students solve conceptual physics questions in simulation-based formative assessments?” The findings showed that the students still used equations to answer the questions. However, their utilizations of equations were different. For example, Alex’s and Christopher’s strategies involved using equations to explain or interpret the given physical situation. To do so, they connected variables to physical situations and provided meanings to the variables and the relationships among the variables. Blake, however, used equations and units as tools to find answers for the questions without a clear connection of the variables and equations to the given physical situations. Christopher’s strategy was especially noticeable in that he used equations as effective explanatory tools for a physical situation. He started an analysis of the physical situation, then translated equations into the situation by creating a physical scenario in a system, such as how variables change as the situation changes, and how the variables are related to each other within the physical system. Alex’s explanations illustrated that he utilized equations to understand a physical situation. The difference between him and Christopher is that Alex used equations as major tools to analyze and understand the situation, while Christopher used them to effectively and easily explain the situation. Noticeably, Alex used algebraic computation processes using an equation to understand a given physical process.
Kuo et al. (2012) argued that linking conceptual reasoning to mathematical formalism indicates a more expert level of understanding and demonstrates robust solutions integrating conceptual and symbolic reasoning. They found that students used equations not just as computational tools but as tools to find conceptual shortcuts to solve physics problems. Although Kuo et al.’s study focused on quantitative problem solving, the current study revealed a similar finding where questions were created qualitatively without asking any calculations. Another difference from Kuo et al.’s study is that they provided an equation to students first, then asked them to explain the equation and apply the equation to a physical situation, whereas the current study provided a physical situation without any equations. As a conclusion, the current study supports that equations can be important in conceptualizing a physical situation by connecting conceptual meanings to equations. Therefore, mathematical equations can be used alternatively in problem solving (Kuo et al., 2012). Redish and Smith (2008) also illuminated the power of equations in solving physics problems and making sense of physical systems when students are able to link physical scenarios to mathematical equations. Thus, the connection of physical meaning to equations should be emphasized in teaching and learning physics in order to help students to conceptualize physical system (Redish & Smith, 2008).
Previous studies of quantitative physics problem solving have focused on using equations first when solving a physics question without a conceptual analysis of the problem situation, which indicated equations were in play as a simple computational tool. Although, the current study found a similar case, in which a student used equations as a simple computational tool, we also found that students used equations as a conceptual understanding or an effective explanatory tool. Indeed, using equations helped Alex realize his misconception and explain the situation accurately. While previous studies have emphasized performing a conceptual analysis first using scientific principles when solving a problem, this study argues the positive roles of using equations when it includes a connection between the equations and the physical situation. Therefore, this study contributes to the literature on physics problem solving in that equations can be used for students as tools for a conceptual understanding and as an explanatory tool. In this study, Christopher’s strategy was closer to the strategy used by experts, since he visualized a given situation to analyze by creating a physical scenario, then connected the relevant equations to the situation to explain the physical scenario. On the other hand, Alex used equations first to answer questions by connecting variables to the physical process through an algebraic solution process. Especially for Alex, equations facilitated his physical understanding of the problem and ability to explain the physical process. Although Alex and Blake used equations primarily as tools to answer questions, Blake did not demonstrate her interpretations of variables or the relationships among them in equations; nor did she connect variables to a physical situation. This indicated that her utilization of equations was closer to simple computational tools.
In conclusion, mathematical equations in physics were important when students were conceptually explaining a physical situation. It was revealed that using equations helped them explain a physical situation with more scientifically normative ideas. However, the ways they used equations differed between students. An equation could be an explanatory tool, a conceptual understanding tool, or a computational tool. The essence of the findings was that when students were able to connect variables to a physical process and to interpret relationships among variables in an equation, equations were in play as tools in understanding and explaining a physical situation. On the other hand, without interpretations of variables and connections to a physical situation, equations only served as simple computational tools. The study also found that students’ strategies to answer questions, especially conceptual ones, did not change with different topics in physics.
Implications and study limitations
As some students pointed out, their physics lectures demonstrated how to solve quantitative questions using equations as computational tools. As Christopher’s problem solving strategy was similar to the strategy used by experts, we suggest that his strategy be reflected in teaching physics. To be more specific, physics educators may provide an opportunity for students to visualize the physics phenomena. They could use models or computer simulations to help this procedure. Second, they should emphasize how equations are used to explain the phenomena as a “conceptual shortcut” (Kuo et al., 2012, p. 39) by connecting equations and variables to the physical situation. In other words, as Alex and Christopher demonstrated, if physics instructions emphasize connections between physical meanings and mathematical expressions, it help students understand physical phenomenon. As we consider physics instructors as experts, perhaps in some cases their expert level of using equations was not reflected in their teaching. A future study topic would be to investigate the reason for the gap between physics experts’ strategies in solving physics problems and their teaching practices when demonstrating how to solve physics problems.
Although the findings of this study suggest an alternative way of using equations as an explanatory or a conceptual analysis tool for a physical situation, the findings might not be generalizable because the study context was limited to an introductory level physics course. Also, it is possible that topics for the tasks (kinematics and mechanical energy conservation) involving several equations might have influenced students’ strategies in answering questions. However, Redish (2017) emphasizes that a goal of physics is to create mathematical modeling (equations) that can predict and explain physical phenomena. Consequently, mathematical equations are included in physics topics and taught extensively in physics instruction especially in high school and college. We argue that students’ understanding of mathematical modeling in physics should not be considered as a following step after conceptual understanding of scientific principles. Instead, we support the claim that blending of physical meaning with mathematical operations should be emphasized in teaching physics (Kuo et al., 2012; Redish, 2005, 2017). We also suggest that future studies should investigate how students’ strategies to answer questions are different in other topics, such as thermodynamics or electricity and magnetism.
Availability of data and materials
Interview data are not available for public.
Abbreviations
- CR:
-
Constructed-Response
- GPE:
-
Gravitational Potential Energy
- KE:
-
Kinetic Energy
- NGSS:
-
Next Generation Science Standards
References
Ardac, D., & Akaygun, S. (2004). Effectiveness of multimedia-based instruction that emphasizes molecular representations on students’ understanding of chemical change. Journal of Research in Science Teaching, 41(4), 317–337.
Chi, M. T. H., Feltovich, P. J., & Glaser, R. (1981). Categorization and representation of physics problems by experts and novices. Cognitive Science, 5, 121–152.
Creswell, J. W. (2016). 30 essential skills for the qualitative researcher. Thousand Oaks: Sage.
Creswell, J. W., & Miller, D. L. (2000). Determining validity in qualitative inquiry. Theory Into Practice, 39, 124–130.
De Cock, M. (2012). Representation use and strategy choice in physics problem solving. Physical Review Special Topics - Physics Education Research, 8(2), 020117.
de Jong, T., & van Joolingen, W. R. (1998). Scientific discovery learning with computer simulations of conceptual domains. Review of Educational Research, 68(2), 179–201.
Dhillon, A. S. (1998). Individual differences within problem-solving strategies used in physics. Science Education, 82(3), 379–405.
Dori, Y. J., & Hameiri, M. (2003). Multidimensional analysis system for quantitative chemistry problems: symbol, macro, micro, and process aspects. Journal of Research in Science Teaching, 40(3), 278–302.
Gick, M. L. (1986). Problem-solving strategies. Educational Psychologist, 21(1–2), 99–120. https://doi.org/10.1080/00461520.1986.9653026.
Gunstone, R. F., Champagne, A. B., & Klopfer, L. E. (1981). Instruction for understanding: a case study: learning research and development center. Pittsburgh: University of Pittsburgh.
Gurel, D. K., Eryılmaz, A., & McDermott, L. C. (2015). A review and comparison of diagnostic instruments to identify students’ misconceptions in science. Eurasia Journal of Mathematics, Science & Technology Education, 11(5), 989–1008.
Huffman, D. (1997). Effect of explicit problem solving instruction on high school students’ problem-solving performance and conceptual understanding of physics. Journal of Research in Science Teaching, 34(6), 551–570.
Kohl, P. B., & Finkelstein, N. D. (2006). Effects of representation on students solving physics problems. Physical Review Special Topics - Physics Education Research, 2(1), 010106.
Kozhevnikov, M., Motes, M. A., & Hegarty, M. (2007). Spatial visualization in physics problem solving. Cognitive Science, 31(4), 549–579.
Kuo, E., Hull, M. M., Gupta, A., & Elby, A. (2012). How students blend conceptual and formal mathematical reasoning in solving physics problems. Science Education, 97(1), 32–57.
Larkin, J. H., McDermott, J., Simon, D. P., & Simon, H. A. (1980). Expert and novice performance in solving physics problems. Science, 208(4450), 1335–1342.
Lazonder, A. W., & Ehrenhard, S. (2014). Relative effectiveness of physical and virtual manipulatives for conceptual change in science: how falling objects fall. Journal of Computer Assisted Learning, 30(2), 110–120.
Maloney, D. P. (1994). Research on problem solving: physics. In D. L. Gabel (Ed.), Handbook of research in science teaching and learning, (pp. 327–354). New York: Macmillan.
McDermott, L. C. (1991). Millikan lecture 1990: What we teach and what is learned—closing the gap. American Journal of Physics, 59, 301–315.
National Research Council (2012). A framework for K-12 science education: practices, crosscutting concepts, and core ideas. Washington, DC: National Academies Press.
National Research Council (2014). Developing assessments for the next generation science standards. Committee on developing assessments of science proficiency in K-12. In W. J. W. Pellegrino, M. R. Wilson, J. A. Koenig, & A. S. Beatty (Eds.), Board on testing and assessment and board on science education. Division of behavioral and social sciences and education. Washington, DC: The National Academies Press.
NGSS Lead States. (2013). Next Generation Science Standards: For states, by states. Washington, DC: The National Academies Press.
Park, M. (2019). Effects of simulation-based formative assessments on students’ conceptions in physics. Eurasia Journal of Mathematics, Science and Technology Education, 15(7), em1722.
Park, M., Liu, X., & Waight, N. (2017). Development of the connected chemistry as formative assessment pedagogy for high school chemistry teaching. Journal of Chemical Education, 94(3), 273–281.
Pellegrino, J. W. (2013). Proficiency in science: Assessment challenges and opportunities. Science, 340(6130), 320–323.
Quellmalz, E. S., Timms, M. J., Silberglitt, M. D., & Buckley, B. C. (2012). Science assessments for all: integrating science simulations into balanced state science assessment systems. Journal of Research in Science Teaching, 49(3), 363–393.
Redish, E. F. (2005). Problem solving and the use of math in physics courses. Delhi: Proceedings of the Conference, World View on Physics Education in 2005: focusing on change.
Redish, E. F. (2017). Analysing the competency of mathematical modelling in physics. In T. Greczyło, & E. Dębowska (Eds.), Key competences in physics teaching and learning, (pp. 25–40). Chum: Springer International Publishing.
Redish, E. F., & Smith, K. A. (2008). Looking beyond content: skill development for engineers. Journal of Engineering Education, 97(3), 295–307.
Rutten, N., van Joolingen, W. R., & van der Veen, J. T. (2012). The learning effects of computer simulations in science education. Computers & Education, 58(1), 136–153.
Simon, D. P., & Simon, H. A. (1978). Individual differences in solving physics problems. In R. S. Sigler (Ed.), Children’s thinking: what develops? (pp. 325–348). Hillsdale: Erlbaum.
Smetana, L., & Bell, R. L. (2012). Computer simulations to support science instruction and learning: a critical review of the literature. International Journal of Science Education, 34(9), 1337–1370.
Srisawasdi, N., & Panjaburee, P. (2015). Exploring effectiveness of simulation-based inquiry learning in science with integration of formative assessment. Journal of Computers in Education, 2(3), 323–352.
Strauss, A. L., & Corbin, J. (1998). Basics of qualitative research: grounded theory procedures and techniques. Newbury Park: Sage.
Treagust, D. F. (1985). Diagnostic tests to evaluate students’ misconceptions in science. French Lick Springs: Paper presented at the annual meeting of the National Association for research in science teaching (NARST).
Trundle, K. C., & Bell, R. L. (2010). The use of a computer simulation to promote conceptual change: a quasi-experimental study. Computers & Education, 54(4), 1078–1088.
Underwood, S. M., Posey, L. A., Herrington, D. G., Carmel, J. H., & Cooper, M. M. (2018). Adapting assessment tasks to support three-dimensional learning. Journal of Chemical Education, 95, 207–217.
van Heuvelen, A. (1991). Learning to think like a physicist: a review of research based instructional strategies. American Journal of Physics, 59, 891–897.
Acknowledgements
None.
Funding
None.
Author information
Authors and Affiliations
Contributions
First and Corresponding author. Dr. MP (100% contribution). Dr. Park designed the study, collected and analyzed data, and wrote the manuscript entirely. The author read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The author declares that he/she has no competing interests
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Park, M. Students’ problem-solving strategies in qualitative physics questions in a simulation-based formative assessment. Discip Interdscip Sci Educ Res 2, 1 (2020). https://doi.org/10.1186/s43031-019-0019-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s43031-019-0019-4